【执行FFT分析】FFT参数详解：窗口类型选择、零填充影响、频率范围设置

首页专栏开发技术【执行FFT分析】FFT参数详解：窗口类型选择、零填充影响、频率范围设置 【执行FFT分析】FFT参数详解：窗口类型选择、零填充影响、频率范围设置 立即解锁 发布时间: 2025-04-16 11:19:42 阅读量: 73 订阅数: 92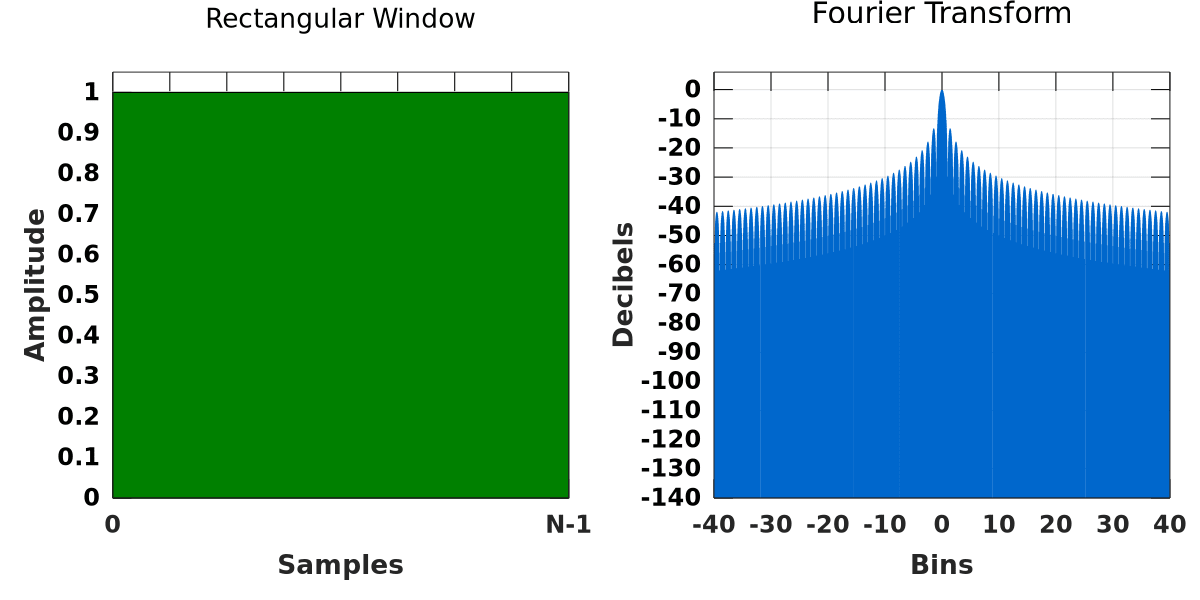 

# 1. 快速傅里叶变换（FFT）基础解析

快速傅里叶变换（FFT）是数字信号处理中的一项核心技术，它允许我们以极高的效率将时域信号转换为频域信号。FFT的出现极大地推动了信号分析和信号处理领域的发展。它的基本原理是利用信号的周期性和对称性来减少离散傅里叶变换（DFT）的计算量。通过利用迭代算法，FFT能够在比DFT更短的时间内完成同样数量数据点的变换。

在本章节中，我们首先介绍FFT的基本概念，然后逐步深入到其算法的核心，包括蝶形运算和位反转等关键技术，最终让读者对FFT有一个全面和基础的认识。

# 2. FFT参数选择的理论基础

2.1 FFT窗口类型的作用与选择

### 2.1.1 窗口类型的基本功能介绍

快速傅里叶变换（FFT）是数字信号处理中的一项基本技术，它能够将时域信号转换为频域信号。窗口函数是FFT分析中一个重要的概念，它用于减少频谱泄露并提高频率分辨率。在进行FFT分析时，由于信号通常被截断，会导致信号的不连续性，从而在频谱中产生泄露现象。这时，窗口函数就起到一个平滑信号的作用，使得信号两端接近零，以减少频谱泄露。

不同的窗口类型对频谱泄露和频率分辨率有不同的影响。例如，矩形窗可以提供最佳的频率分辨率，但会增加频谱泄露；而汉宁窗能够减少频谱泄露，但会牺牲一部分频率分辨率。

### 2.1.2 不同窗口类型对分析结果的影响

选择合适的窗口类型对FFT分析结果至关重要。以下是几种常见窗口类型及其对分析结果的影响：

- **矩形窗（Rectangular Window）**

- 频率分辨率高，但频谱泄露严重。

- **汉宁窗（Hanning Window）**

- 相较于矩形窗，频谱泄露大幅减少，但频率分辨率降低。

- **布莱克曼窗（Blackman Window）**

- 进一步减少频谱泄露，频率分辨率进一步降低，适用于信噪比较低的信号分析。

- **凯泽窗（Kaiser Window）**

- 可以通过调整参数来平衡频谱泄露和频率分辨率，灵活性高。

### 2.2 零填充在FFT中的作用与影响

#### 2.2.1 零填充的基本概念与原理

零填充（Zero-padding）是FFT分析中用于提高频率分辨率的一种技术。在信号序列末尾填充零值，可以使FFT运算得到更多的输出点，从而在频域内产生更精细的频率分辨率。零填充并不改变信号的频谱内容，但它使得频谱中的峰值更尖锐，更容易区分。

#### 2.2.2 零填充对频率分辨率的影响

频率分辨率由FFT的采样频率和输出点数共同决定。具体来说，频率分辨率的计算公式为：

\[ \text{频率分辨率} = \frac{\text{采样频率}}{\text{输出点数}} \]

通过零填充增加输出点数，可以提高频率分辨率。例如，如果原始采样频率为1000 Hz，不进行零填充时输出点数为1024点，则频率分辨率为976.56 mHz；如果进行零填充至4096点，频率分辨率则提高到244.14 mHz。

#### 2.2.3 零填充对频谱泄露的抑制作用

零填充不仅能够提高频率分辨率，还能抑制频谱泄露。通过增加输出点数，可以使每个频率分量的主瓣变窄，从而减少旁瓣的影响，进而降低频谱泄露。

### 2.3 频率范围设置的重要性与方法

#### 2.3.1 频率范围设置的理论依据

FFT分析中的频率范围是由采样频率决定的。根据奈奎斯特定理，最大可分析频率为采样频率的一半，称为奈奎斯特频率。因此，设置频率范围时需要考虑采样频率，并确保分析范围不超过奈奎斯特频率。

#### 2.3.2 如何根据需求正确设置频率范围

正确设置频率范围需要根据分析的目的来决定。以下是设置频率范围的步骤：

1. **确定分析目的：** 首先要明确分析是为了检测信号中的特定频率成分，还是为了观察信号的频谱分布。

2. **参考采样频率：** 根据信号的采样频率，确定奈奎斯特频率。

3. **设置频率范围：** 根据分析目的，选择适当的频率范围，确保不会遗漏重要的频率成分，同时避免超出分析设备的处理能力。

例如，如果采样频率为10 kHz，分析目的是观察信号在1 kHz以下的频谱成分，则频率范围可以设置为0到1 kHz。

在实际操作中，可以通过FFT分析软件或编程实现（例如使用Python中的`numpy.fft`库）进行频率范围的设置和分析。

# 3. FFT参数选择的实战技巧

## 3.1 窗口类型的实际选择与应用案例

### 3.1.1 根据信号特性选择窗口类型

在使用快速傅里叶变换（FFT）进行信号分析时，窗口类型的选择至关重要，因为它直接影响到频谱的分析精度和结果的可靠性。不同的窗口类型适用于不同特性的信号，例如平稳信号、非平稳信号、瞬态信号等。以下是一些常见窗口类型的特性及其适用场景：

- **矩形窗口（Rectangular Window）**：这种窗口类型会使得信号两端产生较大幅度的泄露，但其主瓣宽度较窄，适用于频谱泄露不是主要关注点的场景，且需要较高频率分辨率的分析。

- **汉宁窗口（Hanning Window）**：与矩形窗口相比，汉宁窗口在信号两端的泄露减少了很多，但其主瓣宽度变宽，适用于需要减少频谱泄露的稳定信号分析。

- **汉明窗口（Hamming Window）**：汉明窗口与汉宁窗口类似，但在信号两端的泄露减少程度更大，适用于更加注重减少泄露的场合。

- **布莱克曼窗口（Blackman Window）**：布莱克曼窗口提供了最好的泄露特性，但其主瓣宽度最大，适用于对泄露敏感的分析。

在选择窗口类型时，应当根据信号的特性和分析的需求来综合考虑。例如，对于带有瞬态特性或突变信号，可能需要选择一个频谱泄露较小的窗口以保证频谱的准确性；而对于长期稳定且变化不大的信号，选择一个主瓣宽度较窄的窗口以提高频率分辨率。

### 3.1.2 实际应用中的窗口类型调整技巧

在实际应用中，窗口类型的调整往往需要多次尝试与分析，以找到最优的频谱分析效果。以下是一些调整窗口类型的技巧：

1. **开始于默认窗口**：大多数分析软件或工具都有一个默认的窗口类型，可以从这个开始，作为分析的起点。

2. **性能对比**：改变窗口类型，观察频谱的泄露程度、主瓣宽度以及信噪比的变化，这有助于选择最佳窗口。

3. **变化窗口大小**：在选择窗口类型之后，还可以调整窗口的大小，这会影响频谱的分辨率和泄露程度。

4. **结合零填充策略**：在某些情况下，结合零填充可以进一步优化窗口类型的选择效果。

例如，当我们分析一个含有多个频率分量的信号时，可能需要多次调整窗口大小和类型来观察对频谱分析结果的影响。最终，通过比较不同窗口类型下频谱的清晰度和泄露程度，可以选定最合适的窗口类型。在实际操作中，通过软件工具进行多次FFT分析并观察频谱变化是一个行之有效的办法。

## 3.2 零填充策略的实践与调整

### 3.2.1 零填充的最佳实践方法

零填充是FFT分析中常用的一种方法，目的是通过在信号序列中增加额外的零值来增加采样点数，从而提高频率分辨率。零填充策略的正确实施对于提高FFT分析结果的质量至关重要。以下是一些最佳实践方法：

- **确定合适的填充位数**：零填充的数量取决于所需的频率分辨率。如果要提高频率分辨率，则需要增加填充的零值数量。一般来说，填充的零值数量应为原信号长度的2的幂次方倍，以避免引入不必要的频率成分。

- **避免过填充**：虽然零填充可以提高频率分辨率，但过多的零填充可能导致频谱图上的“棚格效应”，即频谱的离散性变差。应避免这种不必要的填充，因为它会增加计算量而无明显效果。

- **结合窗函数使用**：零填充通常与窗函数结合使用，以减少频谱泄露的影响。在进行零填充时，合理选择窗函数，可以平衡频率分辨率和频谱泄露的矛盾。

例如，在分析一个信号时，如果原始信号的长度为1024点，而需要更高的频率分辨率进行分析，可以尝试增加到2048点甚至更高。这将使得每一个频率分量的间隔减小，从而得到更为精确的频谱图。

### 3.2.2 实际数据处理中的零填充调整实例

在实际数据处理中，零填充的调整需要结合信号的具体情况来进行。以下是一个零填充调整的实例，以帮助理解这一过程：

假设有一个信号长度为1024点，采样频率为1000Hz，目标是提高频率分辨率。根据目标分辨率，我们可以计算出需要填充的零值数量。如果目标分辨率是原始信号分辨率的两倍，则需要将信号长度填充到2048点。这样做的具体步骤可能如下：

1. 将原始信号序列后补充1024个零值，使其长度变为2048点。

2. 应用一个合适的窗函数以减少频谱泄露的影响。

3. 执行FFT变换，得到长度为2048点的频谱数据。

4. 分析频谱数据，观察由于零填充导致的频率分辨率提升。

在这个过程中，零填充的数量和窗函数的选择都是关键因素，它们直接影响到频谱分析的最终结果。实际操作中，可能需要多次调整来找到最优的分析结果。在某些专业的信号处理软件中，零填充和窗函数的选择可以自动完成，但在大多数情况下，需要人工进行干预和调整。

## 3.3 频率范围设置的实战应用

### 3.3.1 频率范围设置的常见误区与排除

在进行FFT分析时，正确设置频率范围是一个重要的步骤，但是由于经验不足或理解不当，使用者可能会陷入一些误区。以下是几个频率范围设置的常见误区及其排除方法：

- **误区一：设置错误的频率范围**。有些人可能会将频率范围设置得过低或过高，导致无法观察到信号中的重要频率分量。为避免这一误区，应根据信号的特性和分析目的来合理设置频率范围。

- **误区二：忽略频率范围的有限性**。由于采样定理，FFT只能分析到奈奎斯特频率（采样频率的一半），因此在设置频率范围时需要考虑这一点。

- **误区三：不考虑频率轴的分辨率**。频率轴的分辨率取决于FFT的点数和采样频率。如果频率分辨率不够，可能导致无法分辨紧邻的频率分量。

排除这些常见误区的关键在于对采样定理的深入理解和对FFT输出结果的正确解读。在实际应用中，应当首先明确信号的采样频率和FFT的点数，然后根据信号特性（如最高频率分量）来确定频率范围。同时，考虑到频率分辨率的限制，适当选择窗函数和零填充策略来提高分辨率。

### 最低0.47元/天 解锁专栏 买1年送3月 继续阅读 点击查看下一篇 400次

会员资源下载次数

300万+

优质博客文章

1000万+

优质下载资源

1000万+

优质文库回答

0 0 复制全文 相关推荐 详解：用matlab如何实现fft变换.doc 执行FFT变换，这里我们对信号进行512点的零填充以提高分辨率： matlab number = 512; y = fft(x, number); n = 0:length(y)-1; f = fs * n / length(y); % 频率轴 然后在子图中显示FFT结果： matlab ... FFT.rar_fft_fft变换 **快速傅里叶变换(FFT)详解** 快速傅里叶变换（Fast Fourier Transform，简称FFT）是一种计算离散傅里叶变换（Discrete Fourier Transform，DFT）的高效算法。在信号处理、图像分析、通信工程、音频处理等多个领域... fft.rar_fft_fft变换 **快速傅里叶变换(FFT)详解** 快速傅里叶变换（Fast Fourier Transform，简称FFT）是一种用于计算离散傅里叶变换（Discrete Fourier Transform，DFT）的有效算法，大大减少了计算量，使得在数字信号处理、图像处理... MATLAB中fft与ifft函数详解：数字信号处理关键工具 MATLAB数字信号处理中的fft函数与ifft函数是进行快速离散傅里叶变换和反变换的核心工具，对于理解和分析数字信号至关重要。fft函数（Fast Fourier Transform）是MATLAB内置的一种高效算法，用于计算离散信号的频域... FFT算法详解：从DIT到IFFT 5. **线性卷积的FFT算法**：通过FFT可以高效地计算两个序列的线性卷积，其基本思想是将两个序列扩展并零填充，然后进行FFT，点乘后逆FFT，最后截取适当长度的结果。 FFT在系统分析和频谱分析中扮演着重要角色。例如... FFT算法设计详解：滤波与低通特性实现 本资源主要介绍了一种基于DSP2833x微控制器的快速傅里叶变换(FFT)设计，用于数字信号处理中的滤波和频谱分析。首先，我们看到一个C语言代码片段，它导入了相关的库文件，如DSP2833x_Device.h、DSP2833x_Examples.h，... MATLAB FFT使用详解与示例：2021年频谱分析指南 - X = FFT(x, N)：可以明确指定输出的点数N，这样可以控制频率分辨率，若N小于x的长度，则进行零填充。 2. 使用注意事项： - FFT返回值具有对称性：在MATLAB中，FFT函数返回的结果通常包含N个元素，... C语言实现详解：快速傅里叶变换(FFT)算法 需要注意的是，FFT_N必须是2的幂，如果不是，可能需要填充额外的零以达到这个要求。 在实际应用中，除了理解基本的算法和实现，还需要考虑性能优化，如使用向量化技术、预计算某些常数以减少计算量等。同时，为了... MATLAB中的FFT谱分析及应用详解 2. 幅值大小与选择的FFT点数有关，但并不影响分析结果。因为IFFT（逆FFT）会自动进行归一化处理。若要获取实际振幅，应将FFT结果乘以2/N。 以下是一个使用FFT进行幅频分析的例子： 考虑信号x=0.5*sin(2*pi*15*t)... C语言实现FFT：快速傅里叶变换详解 通常，一个完整的FFT程序还会包括对输入序列进行预处理（如填充零或对称扩展）以及后处理步骤（如归一化或去除直流偏移）。 这个C语言实现的FFT函数是一个基础的框架，用户需要根据具体需求进行适当的扩展和优化，... 更安全的C语言字符串处理函数 StrSafe.h，位于STANDARDSDK_500/Include/Armv4i/strsafe.h等，每种CPU类型下都有对应的StrSafe.h文件存在。 #include STRSAFEAPI是为了解决现有的 C 语言运行时函数的代码容易产生的“内存溢出”问题而设计的。当引用 strsafe 系列函数时，原有的 C 语言字符串处理函数都将被自动进行 #undef 处理。调试过程 spring-jdbc-4.0.0.RELEASE.jar中文-英文对照文档.zip 1、压缩文件中包含：

中文-英文对照文档、jar包下载地址、Maven依赖、Gradle依赖、源代码...... SW_孙维

开发技术专家 知名科技公司工程师，开发技术领域拥有丰富的工作经验和专业知识。曾负责设计和开发多个复杂的软件系统，涉及到大规模数据处理、分布式系统和高性能计算等方面。

最低0.47元/天 解锁专栏

买1年送3月 百万级

高质量VIP文章无限畅学

千万级

优质资源任意下载

千万级

优质文库回答免费看

立即解锁 专栏目录

【引言与基础知识】快速傅里叶变换的定义：从时域到频域的转换技术

试读

【引言与基础知识】傅里叶变换的历史背景：傅里叶级数与傅里叶积分

试读

【引言与基础知识】离散与连续傅里叶变换的区别与联系

试读

【Origin软件简介】Origin软件概述：数据可视化与分析平台

【Origin软件简介】Origin在数据分析中的应用：数据处理、统计、图形绘制

【FFT前的准备工作】数据格式转换：确保数据适用于FFT分析

【执行FFT分析】FFT参数详解：窗口类型选择、零填充影响、频率范围设置

【结果解读与后处理】FFT结果分析：如何解读幅度谱和相位谱

【FFT在特定应用中的案例分析】音频信号分析：音高与音质的FFT解读

【高级主题】二维FFT的应用：图像处理中的频域转换

【Origin FFT：解锁数字信号处理的神秘力量】：入门到精通的全面教程

快速傅里叶变换(FFT)：从0到1，彻底掌握其原理及应用

【Origin FFT优化秘籍】：提升分析效率的5个实用技巧

【FFT在信号处理中的应用】：Origin实战案例大解析

【Origin FFT进阶应用】：频谱分析的高阶秘诀与自定义技巧

【Origin FFT：频谱解读大师】：深入理解频谱结果的奥秘

【FFT在数据处理中的应用】：Origin案例分析与信号处理技巧

【Origin FFT高级应用】：噪声过滤与信号分离的终极指南

【FFT在生物医学信号处理中的应用】：Origin软件全面教程

【Origin FFT教程：频域与时域的桥梁】：深入理解FFT的奥秘

【FFT参数调整指南】：Origin软件分析效率优化技巧

【Origin FFT应用技巧】：自定义窗口功能的高效使用

【FFT在音频分析中的应用】：Origin软件案例与解读

【Origin FFT：可视化频域分析】：图形化技术深度解析

FFT在振动分析中的应用：Origin软件技术与案例分析

【Origin FFT教程：数据转换的艺术】：掌握时域与频域转换技巧

FFT算法在图像处理中的应用：Origin软件高级使用技巧

【Origin FFT教程：高级案例分析】：复杂信号频域解读秘籍

【FFT在通信系统中的应用】：Origin软件信号调制与解调技术解读

最新推荐 【图像数据预处理高级技巧】：如何运用uniform LBP提升特征质量 

# 摘要

本论文全面介绍了Uniform局部二值模式（LBP）的理论基础、特征提取过程及其在图像数据预处理和深度学习中的应用。文章首先概述了图像数据预处理的重要性，随后深入探讨了LBP的原理及其在图像特征提取中的优势。重点分析了Uniform LBP的提出背景、数学表达和性能优势，以及其在特征提取中的具体步骤和优化策略。此外， 【算法的实验设计】：如何科学评估算法性能 

# 摘要

本文系统介绍了算法性能评估的基础知识，理论分析方法，实验设计原则和方法论，以及实验平台和工具的选择。通过对时间复杂度与空间复杂度的理论分析，算法的最优、平均和最坏情况的性能评估，以及算法稳定性和概率分析的深入探讨，本文为算法性能评估提供了全面的理论支持。接着，本文阐述了实验设计的基本原则、数据收集和处理技术，以及统计分析方法，强调了实验结果的可视化和解释的重要性。在实验平台和工具的选择方面，本文考虑了硬件平台、软件工具、 永久Q钻源码自动化测试框架：提升开发效率与代码质量的秘密 

# 摘要

随着软件开发的快速发展，自动化测试作为保证软件质量的关键环节，其重要性日益凸显。本文详细介绍了永久Q钻源码自动化测试框架的构建与配置、实践技巧以及代码质量提升方法论。文章首先概述了自动化测试的基础理论，并分析了自动化测试框架的组成与核心组件。随后，本文深入探讨了如何搭建自动化测试环境、进行框架代码的模块划分及优化配置。在自动化测试实践技巧章节中，文章提供了测试用例编写、持续集成与部署以及缺 【安全审计】：中国电信物联网平台CA证书审计流程与要点揭秘 

# 摘要

随着物联网技术的快速发展，安全问题成为该领域的核心挑战之一。本文首先概述了物联网平台安全审计的重要性，随后深入分析了CA证书在物联网中的作用，包括其理论基础和在设备身份认证及数据传输加密中的应用。文中还详述了中国电信物联网平台CA证书审计流程，探讨了审计实施的步骤和评估结果。进一步，本文讨论了CA证书审计过程中的关键 步进电机控制秘籍大公开：STM32精确同步技术揭秘 

# 摘要

本文综述了步进电机控制的基础理论、实践技巧以及STM32微控制器在步进电机控制中的应用。首先介绍了步进电机的类型、工作原理和控制理论基础，并探讨了常见的控制问题及其解决方案。接着，阐述了STM32微控制器的功能特点以及如何设计接口与步进电机连接，并详细讲解了编程实现步进电机控制的过程。文中还讨论了精确同步技术的理论基础、实践应用、调试优化方法。最后，分析了步进电机控制的进阶应用，包括微步细分技术、多电机 【Silvaco仿真：纳米技术的应用专题】：探索最新科技领域的创新应用 

# 摘要

本论文全面探讨了Silvaco仿真技术在纳米电子器件设计、纳米结构研究以及能源和生物医学领域中的应用。通过详尽分析纳米材料的电子性质和输运特性，本文揭示了Silvaco仿真在纳米器件模型构建和设计优化中的关键作用。同时，本文深入研究了在光伏、电池材料和能源存储中纳米技术的应用，并探讨了仿 【性能调优攻略】：针对Lenovo B460的BITLAND BM5958固件性能极致优化 

# 摘要

随着计算技术的不断发展，固件性能调优成为了提升硬件性能的关键环节。本文对BITLAND BM5958固件性能调优进行全面概述，从硬件性能调优基础出发，探讨了CPU、GPU以及内存和存储设备的优化原则。文章还深入分析了电源管理策略及其对节能技术应用的影响。在BIOS与固件级调优部分，本文详细讨论了BIOS设置优化以及固件更新对性能和稳定性的改善。操作系统级性能调优涉及系统服务管理与进程优化， 工作流自动化：CAMSTAR MES系统提升工作效率的终极秘籍 # 摘要

本文首先介绍了工作流自动化与CAMSTAR MES系统的基本概念和架构。然后深入解析了CAMSTAR MES系统的组件、功能、部署与实施考量，以及其在工作流自动化、数据集成、实时监控和故障预防维护中的实践应用。文章进一步探讨了CAMSTAR MES系统的高级功能，例如高级排程优化、质量管理与追溯系统、以及报表和分析工具。在案例研究与最佳实践章节中，本文分析了不同行业的MES实施案例，并提取了成功实施的关键因素和面临挑战的应对策略。最后，展望了MES系统的未来趋势以及技术创新带来的变革机遇。

# 关键字

工作流自动化；CAMSTAR MES；系统架构；数据集成；故障预防维护；高级排程 安装不再棘手：transformer_engine在PyTorch环境中的快速部署攻略 

# 1. transformer_engine简介

## 概述：transformer_engine的起源与应用

在深度学习领域，transformer模型以其卓越的性能在自然语言处理(NLP)、计算机视觉等众多应用中占据重要地位。随着模型的复杂性和规模的持续增长，需要更加高效的计算资源和优化算法。transformer_engine应运而生，它为深度学习框架 【Windows Update攻击案例】：如何保护系统不被用作攻击入口 

# 摘要

本文详细探讨了Windows Update攻击的原理和防御策略。首先概述了攻击的途径和原理，包括自动更新机制的弱点以及恶意软件如何利用这一过程。接着，介绍了基础防御措施，如更新管理、系统补丁的安全性，以及网络边界防御与隔离。深入实践中，本文探讨了如何使用安全工具和软件，以及配置Windows Update策略的最优方法。案例研究部分分析了实际攻击的应 资源上传下载、课程学习等过程中有任何疑问或建议，欢迎提出宝贵意见哦~我们会及时处理！

点击此处反馈